The desire to control the investment journey by divsersifying away potential risks has always been a top priority for investors. Steven Goldin of Parala Capital takes a deep dive into the ways investors can manage volatility through a number of factors and the pros and cons of popular methods.
CONTROLLING RISK HAS ALWAYS BEEN A DESIRED OBJECTIVE
Investors have always sought to manage the risks inherent in their portfolios whether through security selection, diversification, asset allocation or insurance. From the simple to the sophisticated, this area of interest has become a source of innovation for index providers and ETFs as they’ve moved beyond cap-weighted beta offerings.
The range of methods being used to control volatility is reasonably broad. In this article, we focus on some of the most popular ones, revealing how they work, the asset types upon which they are applied, the pros & cons and limitations as well as newer methods that are becoming prevalent in the world of indices and will likely soon be available via ETFs as investor interest grows.
Risk control methodologies to be covered can be seen in Table 1 below.
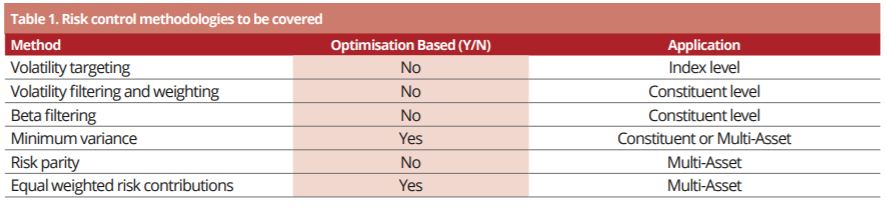
Source: Parala Capital
VOLATILITY TARGETING
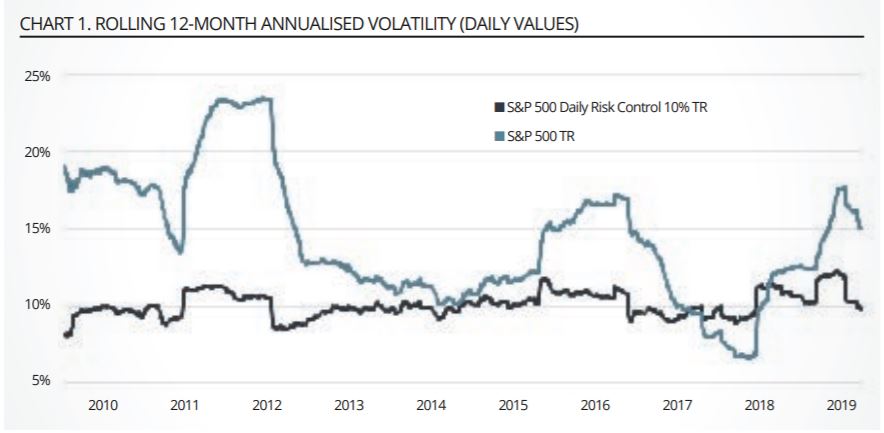
S&P Dow Jones Indices, MSCI, Stoxx and others offer volatility targeted versions of their flagship indices, typically with target volatility levels of 10%, 12% and 15%. They often use “Risk Control” in the name of the index and there are some ETFs that track them like the Japan listed MAXIS TOPIX Risk Control 10% ETF offered by Mitsubishi Asset Management. Linking structured products to these indices is popular with banks active in that business. In fact, many of the methodologies were initially introduced by the banks themselves.
These indices are created by combining a risk asset, say a flagship index, and a riskless asset like Treasury bills. The weight of the risk asset is typically set to equal the target volatility divided by the realised volatility, usually calculated daily over a look back period between 20 to 60 days and often incorporating an exponentially weighted moving average.
For example, if the target volatility was 10% and the realised volatility was 20% than the weight in the risk asset would be 50% (10 divided by 20) and the remaining 50% would be allocated to the riskless asset so that the weights sum to 100%. The advantage of the approach is its relative simplicity, allowing an investor access to their desired index exposure at a volatility level they can tolerate.
Source: Parala Capital
The disadvantage is that the method requires daily rebalancing to maintain the volatility target, making it expensive to implement for all but the most liquid indices. Also, the actual realised volatility of the risk-controlled indices will vary over time due to the estimation error in using historical realised volatility as a proxy for expected volatility of the risk asset.

Source: Parala Capital
VOLATILITY FILTERING AND WEIGHTING
Volatility filtering and weighting is another method that is applied at the index constituent level. It typically involves two steps: (1) selecting the lowest volatility subset of constituents based on a ranking of their historical daily volatility (for example, selecting the 100 lowest volatility constituents) and then (2) weighting each constituent by the inverse of its volatility.
Weighting by the inverse of volatility gives a higher weight to the lowest volatility securities. This method was applied to many flagship indices by leading index providers and proved popular particularly in the US where, for example, ETFs managed by Invesco linked to low volatility versions of the S&P 500, MidCap 400 and SmallCap pulled in over $15 billion in assets through March 2019.
A potential drawback of this method is the selection of the lowest volatility subset leads to different sector concentrations than the parent index so you would be mistaken to think you are getting exposure to a low volatility version of your favourite headline index. Instead, you are getting exposure to the lowest volatility sectors of your favourite headline index.
LOW BETA FILTERING
Low beta filtering is similar to volatility filtering, selecting a subset of the index constituents for example, the highest or lowest 30% based on their historically estimated betas rather than volatility. Typically, this method is applied at the sector or country level to ensure diversification and stocks are still weighted thereafter by their market capitalisation. This method has proven less popular for ETF issuance but there are a few such as the Invesco Russell 1000 Low Beta Equal Weight ETF and some high beta versions that are available to investors.
MINIMUM VARIANCE
Minimum variance optimisation has its roots in the Nobel Prize winning work of Harry Markowitz from his 1952 paper entitled Portfolio Selection. The paper showed that covariance among a universe of securities rather than an individual security’s variance is the critical component to building an ‘optimal’ portfolio with the minimum variance.
Combining securities that have a low correlation with each other provides a diversification benefit which reduces the total variance of a portfolio regardless of each security’s individual level of variance. The method requires the use of a portfolio optimisation tool to solve the ‘problem’ of which combination of securities and weights results in a portfolio with the minimum variance subject to a set of constraints (i.e. minimum or maximum constituent, sector or asset class weights) that might be required.
The method has proven very popular among investors, particularly in Europe with minimum variance ETFs offered by iShares, Lyxor, Ossiam and other leading ETF providers across developed and emerging market as well as regions and countries. There are two challenges to the method. First, a set of potentially subjective constraints must be applied in the optimisation process otherwise the resultant portfolio may have high concentrations in a small number of securities. Second, the method relies on the calculation of a variance-covariance matrix which is prone to higher and higher estimation error the more securities are included in the optimisation.
RISK PARITY
Risk parity is a popular construction method among institutional investors for multi-asset portfolios and benchmarks have been created by S&P Dow Jones Indices among others. Large asset management firms like AQR are big proponents of the approach. Each asset (class) weight is set such that its variance contribution (weight x variance) is the same across all assets. An asset’s risk parity weight can be calculated as 1/volatility of the asset divided by the sum of 1/volatility for all the assets in the portfolio.
It does not require the variance-covariance matrix of all the assets or an optimiser tool to calculate the weights. One of the potential limitations of the approach is that the lowest volatility asset (such as Treasury bills) will end up having a huge weight in the portfolio. Low volatility assets can be excluded or capped but one of the ways that this challenge is often addressed without excluding cash/equivalents is to specify a target volatility such as 5, 7, 10 or 12% for the portfolio.
Leverage is then applied to scale up the weights to achieve the target level of volatility. For practical reasons, futures are often used for the investable universe for this reason.
EQUAL RISK CONTRIBUTION
While risk parity and equal risk contribution share the same basic objective of equal risk weighting, risk parity weights assets inversely to their volatility whereas the equal risk contribution method takes the covariance between assets into account to reduce overall portfolio risk through diversification.
It requires a portfolio optimization tool to arrive at the solution. Several index providers have introduced index families around this concept including FTSE Russell, MSCI and Scientific Beta (Edhec) and ETF launches include the Global X Scientific Beta US ETF which has reached $100 million in assets.
The method is intuitive, but the calculation is complex and prone to estimation errors. First, solving for optimal weights based on equal risk contribution to portfolio variance which itself changes each time a weight is adjusted is circular and may lead to non-linear terms that need additional steps in the optimization process to solve. Second, the method relies on the variance-covariance matrix between securities where estimation error increases with the number of securities which requires sophisticated approaches to address.
CONCLUSIONS
Investors have always been keen to control, manage or diversify away risks in their portfolios. Over recent years, innovations in the world of indexation and ETFs have provided a broadening range of methods to do so and growing array of investable building blocks to
construct portfolios.
Investors should just keep in mind that outcomes from these methods to reduce and/or control risk have variable (and sometimes unexpected) outcomes. This is because the methods for calculating volatility are often backward looking and potential estimation error in calculating covariance increases with the number of securities.
Steven Goldin is founding partner, CEO and co-CIO of Parala Capital
This article first appeared in the Q2 edition of our new publication, Beyond Beta. To receive a full copy, click here.



